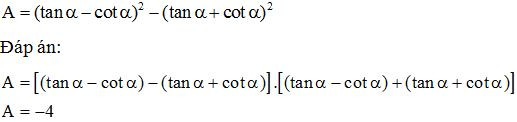50 bài tập về Các bài toán về Tỉ số lượng giác của góc nhọn (có đáp
Các bài toán về Tỉ số lượng giác của góc nhọn và cách giải – Toán lớp 9
A. Lí thuyết
Cho tam giác ABC vuông tại A (như hình vẽ).
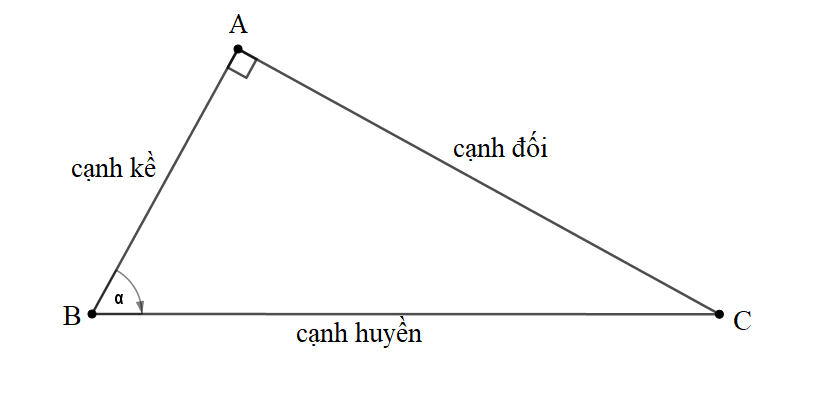
Ta có các tỉ số lượng giác của góc nhọn như sau:
Cách nhớ gợi ý: Sin đi học (đối / huyền) , Cos không hư (kề / huyền), Tan đoàn kết (đối / kề) , Cot kết đoàn (kề / đối).
Các tính chất:
(1) Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
Tức là: Cho hai góc α,β, biết: α+β=90o
Khi đó, ta có:
sinα=cosβ; sinβ=cosα
tanα=cotβ; tanβ=cotα
(2) Nếu hai góc nhọn α, β, có sinα=sinβ hoặc cosα=cosβ thì α=β.
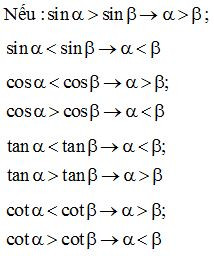
(3) Nếu là một góc nhọn bất kì thì
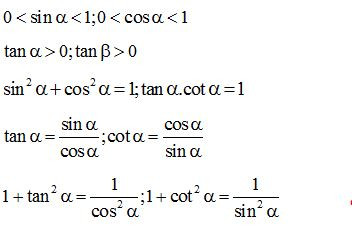
*Bảng giá trị lượng giác các góc đặc biệt
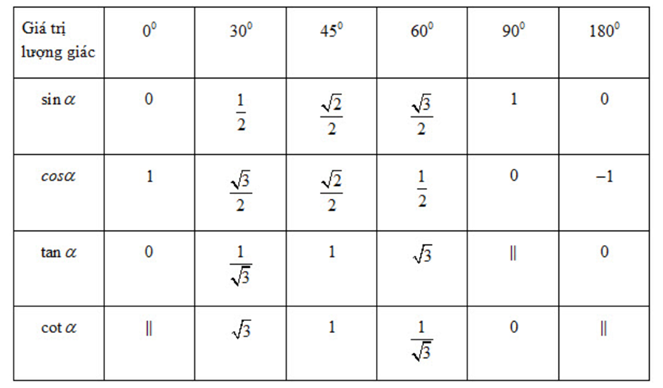
B. Các dạng bài
Dạng 1: Tính toán các tỉ số lượng giác, độ dài các cạnh trong tam giác
Phương pháp giải:
Sử dụng các tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.
Ví dụ minh họa:
Bài 1: Cho tam giác ABC vuông tại B. Có AC = 10cm, cosBAC^=12. Tính sinBAC^ và độ dài AB, BC.
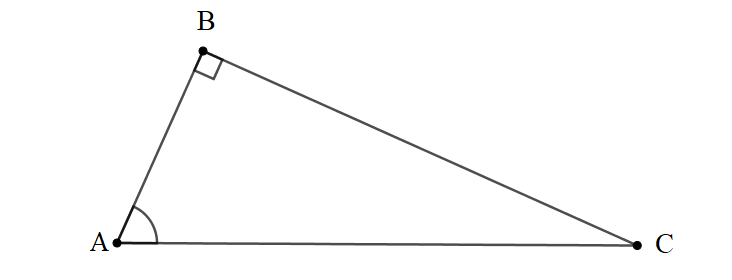
Giải:
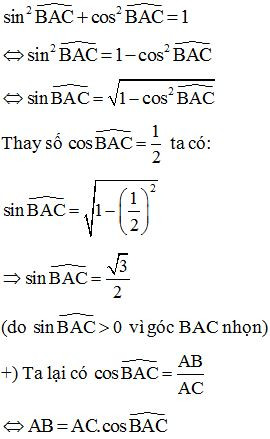
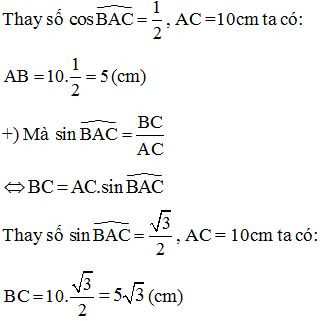
Bài 2: Cho tam giác ABC vuông tại A. Biết AB = 6cm, AC = 8cm. Tính sinABC^, cosABC^, tanABC^, cotABC^.
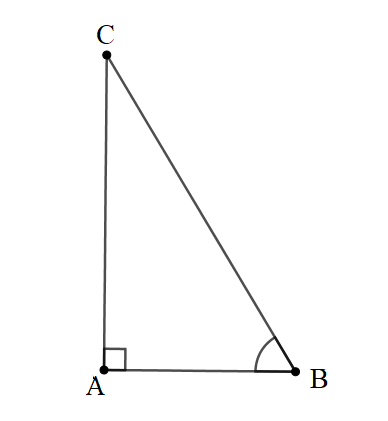
Giải:
Dạng 2: So sánh các tỉ số lượng giác, các góc
Phương pháp giải :
Đưa các tỉ số lượng giác về cùng loại, áp dụng tính chất nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtan góc kia và so sánh dựa trên các tính chất:
Nếu hai góc nhọn α, β, có sinα=sinβ hoặc cosα=cosβ thì α=β.
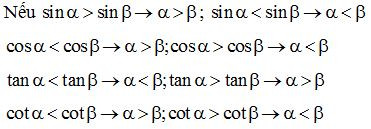
Ví dụ minh họa:
Bài 1: Cho hai góc nhọn α, β. Biết sinα=0,7 và cosβ=32. So sánh α và β.
Giải :
+) Áp dụng tính chất tỉ số lượng giác của góc nhọn ta có:
+) Có cosα≈0,714 < cosβ=32≈0,866⇒α>β
Bài 2: Cho là hai góc nhọn. Biết sinα=cosβ = 0,5. So sánh .
Giải:
+) Áp dụng tính chất tỉ số lượng giác của góc nhọn ta có:
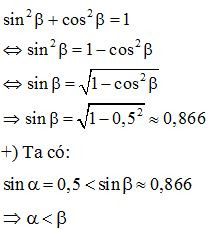
Dạng 3: Rút gọn, tính toán các biểu thức lượng giác
Phương pháp giải:
Áp dụng các tính chất: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtan góc kia. Nếu là một góc nhọn bất kì thì:
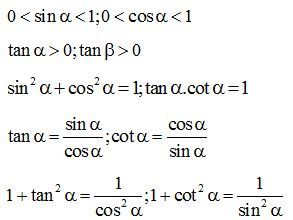
Ví dụ minh họa:
Bài 1: Rút gọn và tính toán biểu thức:
A=sin15o−sin60o+cos30o−cos75o+5
Giải:
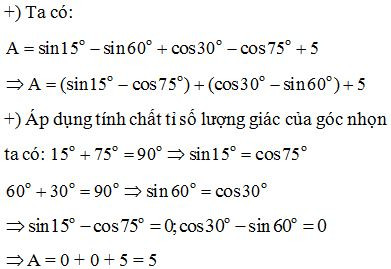
Bài 2: Rút gọn và tính toán biểu thức: A=sin282o+cot24o.cot66o+cos282o
Giải:
Dạng 4: Chứng minh biểu thức, đẳng thức liên quan đến tỉ số lượng giác
Phương pháp giải:
Áp dụng các tính chất: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtan góc kia. Nếu là một góc nhọn bất kì thì:
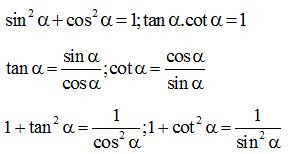
Đối với bài chứng minh biểu thức không phụ thuộc vào giá trị của góc thì cần phải biến đổi sao cho không còn tồn tại các góc trong biểu thức.
Ví dụ minh họa:
Bài 1: Cho hai góc nhọn α, β. Chứng minh rằng: sin4α−cos4β=sin2α−cos2β
Giải:
Bài 2: Cho hai góc nhọn α, β. Chứng minh rằng biểu thức sau không phụ thuộc vào giá trị của α, β: B=cos2α.cos2β+cos2α.sin2β+sin2α
Giải:
C. Bài tập tự luyện
Bài 1: Cho tam giác ABC vuông tại A. Biết AB=6cm, BC=10cm. Tính sinABC^, sinACB^, cosABC^, cosACB^.
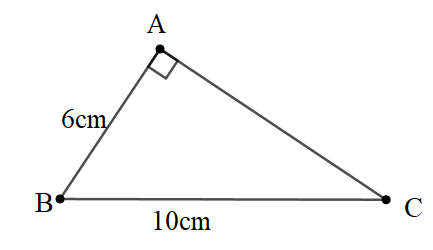
Đáp án: sinABC^=45; sinACB^=35; cosABC^=35; cosACB^=45
Bài 2: Cho tam giác ABC vuông tại A. Có AB=3cm, AC=4cm. Tính tanABC^, tanACB^, cotABC^, cotACB^.
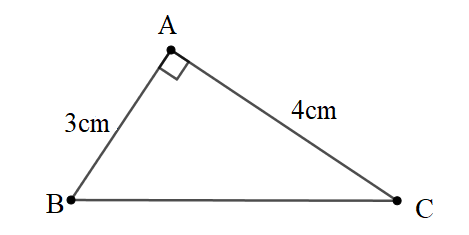
Đáp án: tanABC^=43;tanACB^=34; cotABC^=34;cotACB^=43
Bài 3: Cho tam giác ABC. Có đường cao AH ứng với cạnh BC. AH=5cm, AB=7cm. Tính sinABH^, cosABH^
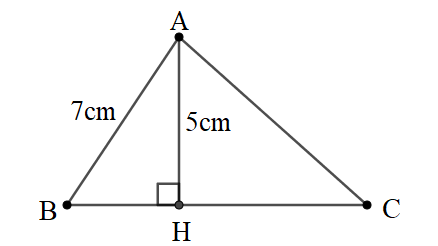
Đáp án: sinABH^=57;cosABH^=267
Bài 4: So sánh các tỉ số lượng giác của hai góc 67° và 54° (không dùng máy tính)
Đáp án: sin67o>sin54o; cos67o<cos54o; tan67o>tan54o; cot67o<cot54o
Bài 5: Cho hai góc nhọn α, β. Biết cotα<cotβ. So sánh số đo α và β
Đáp án: α>β
Bài 6: Cho hai góc nhọn α, β. Nhận định nào sau đây là đúng ?
Đáp án: A
Bài 7: Rút gọn và tính giá trị biểu thức:
Đáp án: A = 1
Bài 8: Rút gọn và tính giá trị biểu thức:
Đáp án: B = 11
Bài 9: Rút gọn và tính giá trị biểu thức:
Đáp án: C = 20
Bài 10: Cho hai góc nhọn . Chứng minh đẳng thức:
sin4α+cos2α.sin2α+sin2α=2sin2α
Đáp án: VT=sin2α(sin2α+cos2α)+sin2α=2sin2α=VP
Bài 11: Cho hai góc nhọn .Chứng minh đẳng thức:
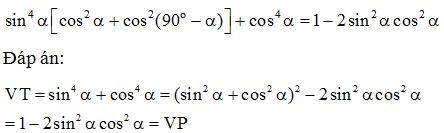
Bài 12: Cho hai góc nhọn α, β. Chứng minh biểu thức sau không phụ thuộc vào giá trị α, β
Theo dõi chúng tôi www.hql-neu.edu.vn để có thêm nhiều thông tin bổ ích nhé!!!
