Các dạng toán về Tỉ lệ thức và cách giải | Toán lớp 7 – vietjack.me
Các dạng toán về Tỉ lệ thức và cách giải – Toán lớp 7
I. LÝ THUYẾT:
1. Định nghĩa:
Tỉ lệ thức là đẳng thức của hai tỉ số ab=cd .
Hay được viết: a:b=c:d . Trong đó a, d là các số hạng ngoài (ngoại tỉ), b, c là các số hạng trong (trung tỉ).
2. Tính chất:
Tính chất 1: Nếu ab=cd thì ad = bc.
Tính chất 2: Nếu ad = bc và a, b, c, d ≠ 0 thì ta có các tỉ lệ thức:
II. CÁC DẠNG BÀI TẬP CƠ BẢN:
Dạng 5.1: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên.
1. Phương pháp giải:
– Viết các số hữa tỉ dưới dạng phân số.
– Thực hiện phép chia phân số.
2. Ví dụ minh họa:
Ví dụ 1: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên.
a) 0,26 : 0,65
b)313:10
Giải:
a) Ta có: 0,26 : 0,65 = 26100:65100=26100.10065=25
Vậy tỉ số giữa hai số hữu tỉ 0,26 : 0,65 bằng tỉ số giữa hai số nguyên 2 : 5.
b) Ta có:313:10=103:101=103.110=13
Vậy tỉ số giữa hai số hữu tỉ 313:10 bằng tỉ số giữa hai số nguyên 1:3.
Dạng 5.2: Lập tỉ lệ thức từ các tỉ số cho trước.
1. Phương pháp giải:
– Xét xem hai tỉ số đã cho co bằng nhau không?
– Nếu hai tỉ số bằng nhau thì chúng lập thành một tỉ lệ thức.
2. Ví dụ minh họa:
Ví dụ 2: Các tỉ số sau đây có lập thành một tỉ lệ thức hay không?
35:6và45:8
Giải:
Dạng 5.3: Lập tỉ lệ thức từ đẳng thức cho trước, từ một tỉ lệ thức cho trước, từ các số cho trước.
1. Phương pháp giải:
Lập tỉ lệ thức từ đẳng thức cho trước:
Nếu ad = bc và abcd ≠ 0 thì ta có các tỉ lệ thức:
Lập tất cả các tỉ lệ thức từ một tỉ lệ thức cho trước:
Từ tỉ lệ thức ab=cd ta có thể lập được ba tỉ lệ thức nữa bằng cách:
– Giữ nguyên ngoại tỉ, đổi chỗ các trung tỉ: ac=bd
– Giữ nguyên trung tỉ, đổi chỗ các ngoại tỉ: db=ca
– Đổi chỗ các ngoại tỉ với nhau, các trung tỉ với nhau: dc=ba
Lập tỉ lệ thức từ các số cho trước: Từ các số đã cho, trước hết phải lập được đẳng thức dạng ad = bc. Sau khi có đẳng thức này, áp dụng tính chất 2 để lập các tỉ lệ thức.
2. Ví dụ minh họa:
Ví dụ 3: Lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:
2,3.4,5 = 1,5.6,9
Giải:
Các tỉ lệ thức có thể được từ các đẳng thức 2,3.4,5 = 1,5.6,9 là:
Dạng 5.4: Tìm số hạng chưa biết của một tỉ lệ thức.
1. Phương pháp giải:
Trong một tỉ lệ thức, ta có thể tìm một số hạng chưa biết khi biết ba số hạng kia.
2. Ví dụ minh họa:
Ví dụ 4: Tìm x trong các tỉ lệ thức sau:
a) 2,57,5=x0,6
b)345:40815=0,25:x
Giải:
III. BÀI TẬP VẬN DỤNG:
Bài 1: Lập tất cả các tỉ lệ thức có thể có từ các đẳng thức sau:
a) 12.20 = 15.16
b) -515=-1,23,6
c) 2,4.3,2 = 8.0,96
Bài 2: Các tỉ số sau đây có lập thành một tỉ lệ thức hay không? Giải thích.
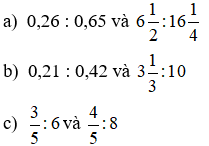
Bài 3: Lập tất cả các tỉ lệ thức từ 4 số sau: 0,25; 1,25; 12; 60.
Bài 4: Lập tất cả các tỉ lệ thức có thể được từ 4 trong 5 số sau:
a) 2; 8; 32; 128; 512
b) 1; 5; 25; 125; 625
Bài 5: Tìm x trong các tỉ lệ thức:
a) 2,5:7,5= x: 35
b) x : 2,5 = 0,003 : 0,75
c) 56:x=20:3
Bài 6: Tìm số hữu tỉ x trong tỉ lệ thức:
Bài 7: Cho tỉ lệ thức 3x-yx+y=34. Tìm giá trị của tỉ số xy .
Bài 8: Bộ bốn số nào dưới đây có thể lập thành một tỉ lệ thức?
a) 4612;6035;7712và 101;
b) -18;56;-4,5 và 31,5.
c) (1 + 2 + 3)2; (1 + 2 + 3)3; 13 + 23 + 33 và 13. 23. 33
Bài 9: Biết rằng tx=43;zx=16 . Tìm tỉ số:tz.
Bài 10: Tính a+bc+b, khi biết ba=2 và cb=3
Hướng dẫn giải:
Bài 1: Các cặp tỉ lệ thức lập được từ các đẳng thức là:
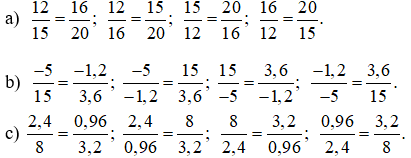
Bài 2: Đáp án:
a) Có vì 0,26:0,65=612:1614
b) Không.
c) Có vì 35:6=45:8
Bài 3: Ta có: 0,25.60 = 1,25.12.
Từ đó suy ra các tỉ lệ thức:
Bài 4: Các cặp tỉ lệ từ 4 trong số là:
a) 2.512 = 8.128
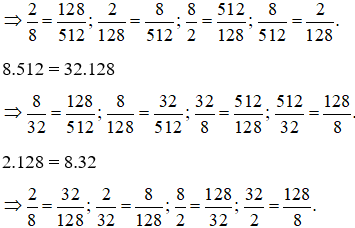
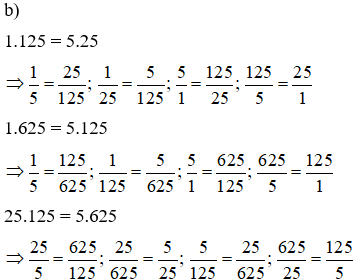
Bài 5:
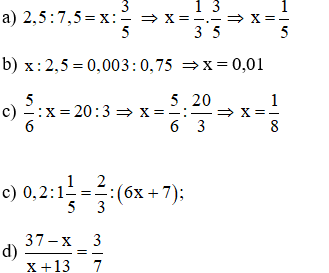
Bài 6: Đáp án:
a) x = 3 b) x=95
c)x=-12 d) x = 22
Bài 7:
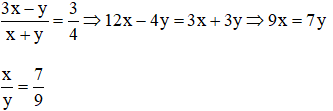
Bài 8:
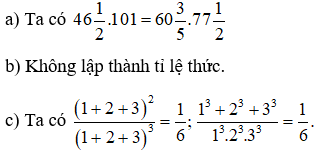
Bài 9:
Bài 10:
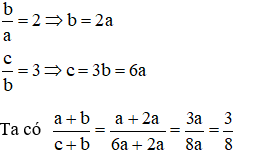
Xem thêm các dạng bài tập và công thức Toán lớp 7 hay, chi tiết khác:
Theo dõi chúng tôi www.hql-neu.edu.vn để có thêm nhiều thông tin bổ ích nhé!!!
