Biến đổi đơn giản biểu thức chứa căn bậc hai – Cùng Toppy chia sẻ

Ở phần Toán học Đại số lớp 9, chúng ta sẽ được làm quen với các kiến thức liên quan đến biểu thức chứa căn bậc 2. Trong đó, yêu cầu bạn phải biết biến đổi đơn giản biểu thức chứa căn bậc hai. Việc biến đổi biểu thực được thực hiện theo phương pháp nào? Có những dạng bài toán nào liên quan đến biến đổi đơn giản biểu thức chứa căn thức bậc hai? Cùng Toppy tìm hiểu nhé.

Đưa thừa số ra ngoài dấu căn cách biến đổi đơn giản biểu thức chứa căn

Cách biến đổi đơn giản biểu thức chứa căn bậc hai đầu tiên đó là đưa thừa số ra bên ngoài dấu căn. Cụ thể:

Với hai biểu thức A, B mà B ≥ 0 ta có √ (A2B) = |A| √ B

Tức là:

Nếu A ≥ 0 và B ≥ 0 thì √ (A2B) = A√ B

Nếu A < 0 và B ≥ 0 thì √ (A2B) = – A√ B

Ví dụ: Với x ≥ 0 ta có: √ (42×2) = √ (3.16×2) = √ [(4x)2.3] = 4x√ 3

Đưa thừa số vào trong dấu căn

Với A ≥ 0 và B ≥ 0 thì A√ B = √ (A2B)

Với A < 0 và B ≥ 0 thì A√ B = – √ (A2B)

Ví dụ: Với x < 0 ta có: x√ 3 = √ (3×2)

Khử mẫu của biểu thức lấy căn

Cách biến đổi đơn giản biểu thức chứa căn bậc hai theo phương pháp này như sau:

Với hai biểu thức A, B mà A B ≥ 0 và B ≠ 0, ta có:

√ (A – B) = √ (A . B) / |B|

Ví dụ: Với x ≠ 0 ta có: √ (11 – x) = √ (11.x) / |x|

Trục căn thức ở mẫu

Với hai biểu thức A, B mà B>0, ta có:

A / √ B = A√ B / B

Với các biểu thức A, B, C mà A ≥ 0 và A ≠ B2, ta có:

Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0 và A ≠ B, ta có:

Ví dụ: Toán 9 biến đổi đơn giản biểu thức chứa căn thức bậc hai

Trục căn thức ở mẫu của biểu thức với x ≥ 0

Ta có:

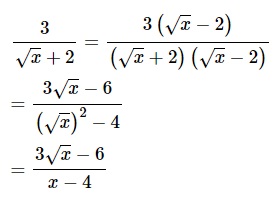
Biến đổi đơn giản biểu thức chứa căn bậc hai bằng cách rút gọn

Bước 1: Dùng các phép biến đổi đơn giản để đưa các căn thức bậc hai phức tạp thành căn thức bậc hai đơn giản.

Bước 2: Thực hiện các phép tính theo thứ tự đã biết.

Ví dụ: Sắp xếp các số sau theo thứ tự tăng dần:

a, 5√ 2; 2√ 5; 2√ 3; 3√ 2

b, √ 27; 6√ (1/3) ; √ 28; √ 53

Lời giải:

a. Đưa thừa số vào trong dấu căn ta được:

5√ 2 = √ 50; 2√ 5 = √ 20; 2√ 3 = √ 12; 3√ 2 = √ 18

Mà √ 12 < √ 18 < √ 20 < √ 50

⇒ 2√ 3 < 3√ 2 < 2√ 5 < 5√ 2

b. Đưa thừa số vào trong dấu căn ta được:

6√ 1/3 = √ 12 ; 2√ 8 = √ 32 ; 5√ 3 =√ 75

Mà √ 12 < √ 27 < √ 32 < √ 75

⇒ 6√ 1/3 < √ 27 < √ 28 < √ 53

Nhận xét: Khi so sánh các căn thức với nhau, ta nên đưa các thừa số vào trong dấu căn, sau đó mới so sánh.

>> Xem thêm: Rút gọn biểu thức lớp 9

Chia sẻ những mẹo hay giúp nhớ lâu các công thức Toán học

Để nắm vững các kiến thức Toán học cũng như biến đổi đơn giản biểu thức chứa căn bậc hai, Toppy xin chia sẻ đến bạn một vài bí quyết sau đây:

Rèn luyện sự tập trung

Tập trung là điều đầu tiên bạn cần làm khi học Toán. Có như vậy, chúng ta mới đạt được hiệu quả cao trong học tập. Đối với môn Toán, khi giải một bài tập, bạn cần phải vận dụng nhiều dạng kiến thức khác nhau. Bước này sẽ có liên quan đến bước kia. Chỉ cần sai một bước là những phần sau cũng sẽ sai theo. Vì thế, điều đầu tiên cần làm khi học Toán là phải tập trung cao độ.

Nắm vững kiến thức

Muốn học tốt một cái gì đó bạn cần phải nắm vững kiến thức. Tuy nhiên, không phải công thức toán học nào cũng dễ nhớ. Nếu bạn không thể nhớ nổi thì cũng “ép buộc” bản thân ghi nhớ sau đó tìm hiểu chúng sau này. Thực hành chính là cách ghi nhớ hiệu quả nhất.

Nhắc lại nhiều lần

Nhắc càng nhiều nhớ càng lâu. Vậy nhắc bằng cách nào? Trước hết, hãy học để hiểu chứ không nên học vẹt. Đồng thời thỉnh thoảng hãy nhắc lại chúng để ghi nhớ một cách dễ dàng hơn.

Làm thật nhiều bài tập

Bài tập chính là chìa khóa giúp bạn ghi nhớ được công thức toán học một cách tối ưu nhất. Ví dụ như khi chúng ta tìm hiểu về biến đổi đơn giản biểu thức chứa căn bậc hai phần lý thuyết chỉ chiếm một lượng nhỏ còn lại là ví dụ và bài tập.

Một phần kiến thức nhưng lại có rất nhiều dạng bài tập khác nhau. Đôi khi còn lồng ghép với cả kiến thức khác. Để có thể học tập hiệu quả nhất thì phải thực hành thật nhiều.

Ghi nhớ bằng cách của riêng mình

Mỗi người sẽ có một cách ghi nhớ khác nhau. Ví dụ như làm sơ đồ tư duy, sử dụng hình vẽ hoặc làm thơ như các ví dụ dưới đây.

Ví dụ công thức Toán tính diện tích hình thang:

“Ta đem đáy nhỏ đáy to cộng vào

Rồi đem nhân với đường cao

Chia đôi kết quả thế nào cũng ra”

Ví dụ công thức hệ thức lượng trong tam giác:

Sao Đi Học ( “Sin = (Đối / Huyền)

Cứ Khóc Hoài ( Cos = Kề / Huyền)

Thôi Đừng Khóc ( Tan = Đối / Kề)

Có Kẹo Đây ( Cotan = Kề/ Đối)”

Học Toán sẽ thú vị hơn rất nhiều nếu bạn biết cách làm chủ các kiến thức mà mình thu nhận được. Cùng tìm hiểu thêm các dạng bài tập về biến đổi đơn giản biểu thức chứa căn bậc hai và các kiến thức khác tại https://toppy.vn/ để học tốt hơn bộ môn này.

Xem thêm:

• Liên hệ giữa phép chia và phép khai phương – Học toán 9
• Phương trình quy về phương trình bậc nhất bậc hai – Học Toán 9
• Liên hệ giữa phép nhân và phép khai phương – Học tốt Toán cùng

Giải pháp toàn diện giúp con đạt điểm 9-10 dễ dàng cùng Toppy

Với mục tiêu lấy học sinh làm trung tâm, Toppy chú trọng việc xây dựng cho học sinh một lộ trình học tập cá nhân, giúp học sinh nắm vững căn bản và tiếp cận kiến thức nâng cao nhờ hệ thống nhắc học, thư viện bài tập và đề thi chuẩn khung năng lực từ 9 lên 10.

Kho học liệu khổng lồ

Kho video bài giảng, nội dung minh hoạ sinh động, dễ hiểu, gắn kết học sinh vào hoạt động tự học. Thư viên bài tập, đề thi phong phú, bài tập tự luyện phân cấp nhiều trình độ.Tự luyện – tự chữa bài giúp tăng hiệu quả và rút ngắn thời gian học. Kết hợp phòng thi ảo (Mock Test) có giám thị thật để chuẩn bị sẵn sàng và tháo gỡ nỗi lo về bài thi IELTS.

Nền tảng học tập thông minh, không giới hạn, cam kết hiệu quả

Chỉ cần điện thoại hoặc máy tính/laptop là bạn có thể học bất cứ lúc nào, bất cứ nơi đâu. 100% học viên trải nghiệm tự học cùng TOPPY đều đạt kết quả như mong muốn. Các kỹ năng cần tập trung đều được cải thiện đạt hiệu quả cao. Học lại miễn phí tới khi đạt!

Tự động thiết lập lộ trình học tập tối ưu nhất

Lộ trình học tập cá nhân hóa cho mỗi học viên dựa trên bài kiểm tra đầu vào, hành vi học tập, kết quả luyện tập (tốc độ, điểm số) trên từng đơn vị kiến thức; từ đó tập trung vào các kỹ năng còn yếu và những phần kiến thức học viên chưa nắm vững.

Trợ lý ảo và Cố vấn học tập Online đồng hành hỗ trợ xuyên suốt quá trình học tập

Kết hợp với ứng dụng AI nhắc học, đánh giá học tập thông minh, chi tiết và đội ngũ hỗ trợ thắc mắc 24/7, giúp kèm cặp và động viên học sinh trong suốt quá trình học, tạo sự yên tâm giao phó cho phụ huynh.