Cách giải phương trình bậc bốn cực hay & các dạng bài tập thường

Cách giải phương trình bậc bốn cực hay & các dạng bài tập thường gặp

Lý thuyết về phương trình bậc bốn cũng như cách giải phương trình bậc bốn là phần kiến thức vô cùng quan trọng của chương trình Đại số 10. Nhằm giúp quý thầy cô cùng các bạn học sinh có thêm nguồn tư liệu quý phục vụ quá trình dạy và học, Tmdl.edu.vn đã chia sẻ bài viết sau đây. Ở đây, ngoài kiến thức cần ghi nhớ còn có nhiều dạng bài tập thường gặp của dạng toán này. Các bạn tìm hiểu nhé !

I. PHƯƠNG TRÌNH BẬC BỐN LÀ GÌ?

Bạn đang xem bài: Cách giải phương trình bậc bốn cực hay & các dạng bài tập thường gặp

Phương trình bậc bốn dạng tổng quát là phương trình có bậc cao nhất là bậc bốn. Thông thường sẽ có đủ các dạng phương trình bậc ba, bậc hai, bậc nhất, không bậc, trong một số bài toán có thể dạng không đầy đủ.

II. CÁC CÁCH GIẢI PHƯƠNG TRÌNH BẬC BỐN CỰC HAY

1. Công thức nghiệm tổng quát của phương trình bậc 4

Dụng ý của ta là phân tích đa thức x4+ax3+bx2+cx+d thành hai nhân tử bậc hai

Dùng ẩn phụ h, ta biến đổi như sau:

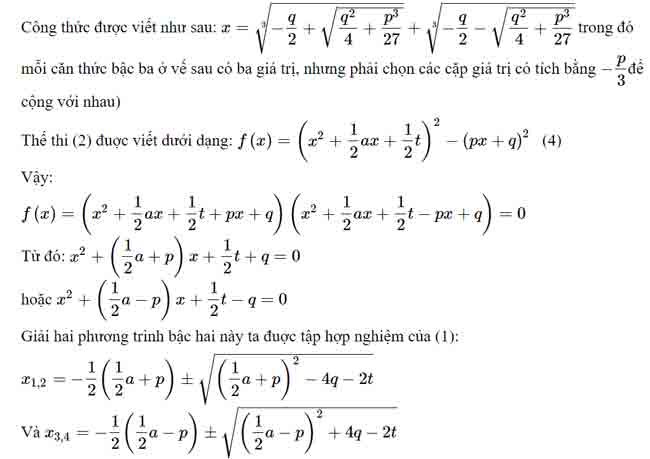
Ví dụ

Giải phương trình: x4−x3−7×2+x+6=0

Giải:Dựa vào công thức (3) ta xác định đuợc h:

2. Phân tích đa thức thành nhân tử bằng phương pháp hệ số bất định.

Ví dụGiải phương trình:

x4+4×3−10×2+37x−14=0 (1)

Giải:

Ta thử phân tích vế trái thành hai nhân tử bậc hai x2+px+q và x2+rx+s , trong đó

p,q,r,s là các hệ số nguyên chưa xác định.

Ta có:

x4+4×3−10×2+37x−14=(x2+px+q)(x2+rx+s) (2)

Đồng nhất các hệ số của những số hạng cùng bậc hai vế của đồng nhất thức ta có hệ phương trình sau

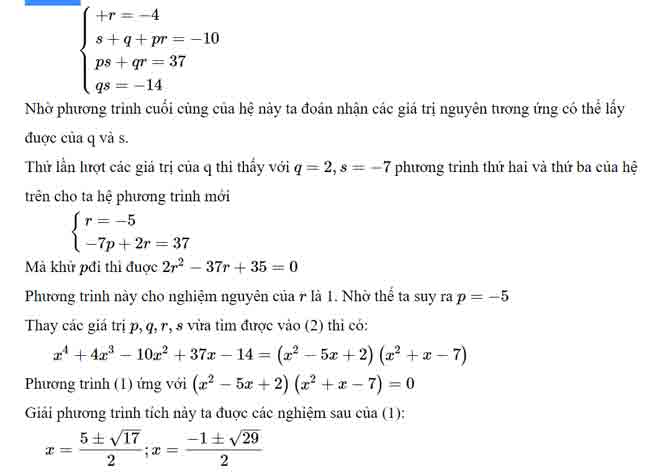
Lưu ý:

Trong một số truờng hợp ta không thể dùng phương pháp này vì nhiều khi việc phân tích trên không được như mong muốn chẳng hạn khi hệ trên không có nghiệm nguyên.

3. Biến đổi hợp lí và sáng tạo trong một số trường hợp cụ thể.

Ví dụ 1Giải phương trình (x2−a)2−6×2+4x+2a=0 (1)

Giải:Phương trình (1) được viết thành

x4−2ax2+a2−6×2+4x+2a=0

hay x4−(2a+6)x2+4x+a2+2a=0 (2)

Phương trình (2) là phương trình bậc bốn đối với x mà bạn không đuợc học cách giải.Nhưng ta lại có thể viết phương trình (1) dưới dạng

a2−2(x2−1)a+x4−6×2+4x=0 (3)

Và xem (3) là phương trình bậc hai đối với a.Với cách nhìn này, ta tìm được a theo x:

Ví dụ 2.Giải phương trình x4−x3−5×2+4x+4=0 (1)

Giải:Phương trình (1) đuợc viết dưới dạng:

−x3−x2−(4×2−4x−4)=0

x2(x2−x−1)−4(x2−x−1)=0

(x2−4)(x2−x−1)=0

Vậy (1) có 4 nghiệm là

Ví dụ 3.Giải phương trình 32×4−48×3−10×2+21x+5=0 (1)

Giải:Ta viết (1) dưới dạng:

2(16×4−24×3+9×2)−7(4×2−3x)+5=0

Và đặt: y=4×2−3x thì (1) được biến đổi thành

2y2−7y+5=0

Từ đó y1=1 và y2=5/2

Giải tiếp các phương trình bậc hai đối với x sau đây (sau khi thay y1=1 và y2=5/2 vào y=4×2−3x ):

4×2−3x−1=0

Và 8×2−6x−5=0

Ta sẽ đuợc các nghiệm của (1).

Ví dụ 4. Giải phương trình

2×4+3×3−16×2+3x+2=0 (1)

Giải:

Đây là phương trình bậc bốn (và là phương trình hồi quy khi e/a=(d/b)2)

Với phương trình này ta giải như sau:Chia hai vế của phương trình cho x2 (khác không) thì (1) tương đuơng với

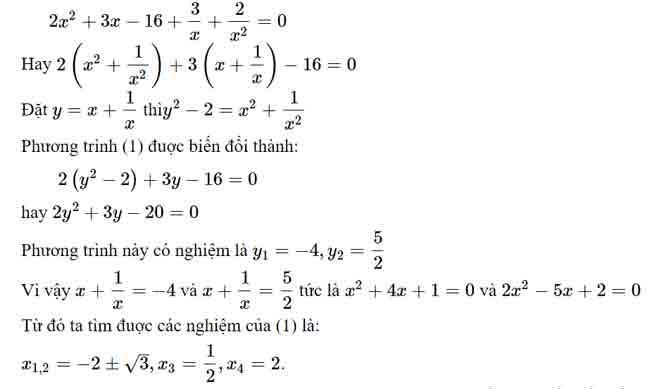
Như vậy, với các ví dụ 2,3 và 4 ta giải đuợc phương trình bậc bốn nhờ biết biến đổi sáng tạo vế trái của phương trình để dẫn tới việc giải các phương trình và phương trình quen thuộc.

4. Phương pháp đồ thị.

Phương pháp:

Để giải phương trình bậc bốn

x4+ax3+bx2+cx+d=0 (1)

bằng đồ thị, ta hãy đặt x2=y−mx

Phương trình (1) trở thành: y2−2mxy+m2x2+axy−axm2+bx2+cx+d=0

Để khử đuợc các số hạng có xy trong phương trình này thì phải có:

Vậy là các bạn vừa được chia sẻ lý thuyết về phương trình bậc bốn cũng như cách giải phương trình bậc bốn cực hay. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu quý. Chia sẻ thêm cách giải phương trình bậc ba tại đường link này bạn nhé !!

Bản quyền bài viết thuộc trường Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận! Nguồn chia sẻ: Trường Tmdl.edu.vn (tmdl.edu.vn)

Trang chủ: tmdl.edu.vn Danh mục bài: Giáo dục