Chuyên đề hình thang cũng như cách chứng minh hình thang là phần kiến thức trọng tâm của Hình học 8. Bài viết hôm nay, Zicxabooks.com.vn sẽ giới thiệu đến quý thầy cô cùng các em những kiến thức cần ghi nhớ về hình thang và cách chứng minh hình thang nhanh chóng. Bạn tìm hiểu nhé !
I. LÝ THUYẾT VỀ HÌNH THANG
1. Định nghĩa:
Hình thang là một tứ giác lồi có 2 cạnh đối song song. Hai cạnh này được gọi là hai cạnh đáy của hình thang. Hai cạnh còn lại là hai cạnh bên,
Các trường hợp đặc biệt của hình thang:
- Hình thang vuông: Hình thang có 1 góc vuông được gọi là hình thang vuông
- Hình thang cân: Hình thang có 2 góc kề một cạnh đáy bằng nhau là hình thang cân.
- Hình thang vuông cân: Là hình thang vừa vuông vừa cân và còn được gọi là hình chữ nhật.

2. Các tính chất của hình thang
Tính chất về góc:
- Hai góc kề một cạnh bên của hình thang có tổng bằng 180 độ (nằm ở vị trí trong cùng phía của hai đoạn thẳng song song là 2 cạnh đáy).
- Đối với hình thang cân thì hai góc kề một cạnh đáy bằng nhau.
Tính chất về cạnh:
- Hình thang có 2 cạnh đáy bằng nhau thì hai cạnh bên sẽ song song và bằng nhau.
- Ngược lại, nếu hình thang có 2 cạnh bên song song thì chúng sẽ bằng nhau và 2 cạnh đáy bằng nhau.
- Hình thang cân có 2 đường chéo bằng nhau.
Tính chất về đường trung bình:
Đường trung bình là đường thẳng nối trung điểm hai cạnh bên của hình thang.
- Tính chất 1: Đường thẳng đi qua trung điểm 1 cạnh bên của hình thang và song song với 2 cạnh đáy thì sẽ đi qua trung điểm của cạnh bên còn lại.
- Tính chất 2: Đường trung bình của hình thang sẽ song song với 2 cạnh đáy và bằng ½ tổng 2 đáy.
3. Các loại hình thang
Hình thang vuông:
Hình thang vuông là hình thang có một góc vuông

Hình thang cân:
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau
Trong hình thang cân, hai cạnh bên bằng nhau.
Trong hình thang cân, hai đường chéo bằng nhau.
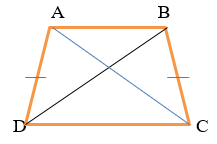
4. Dấu hiệu nhận biết hình thang cân
- Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
II. CÁCH CHỨNG MINH HÌNH THANG NHANH NHẤT
– Cách 1: Chứng minh tứ giác đó có một cặp cạnh đối song song.
Ví dụ: Cho hình thang ABCD (AB // CD). Gọi E là giao điểm của hai đường thẳng AD và BC. Gọi M, N, P, Q theo thứ tự là các trung điểm của các đoạn thẳng AE, BE, AC và BD. Chứng minh tứ giác MNPQ là hình thang.
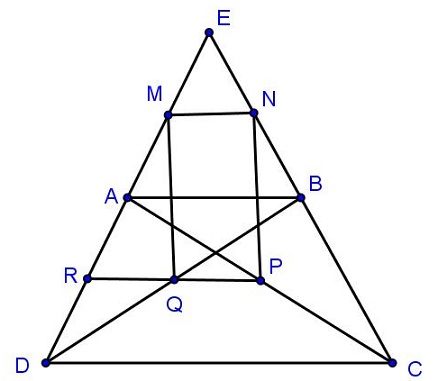
Ta có:
M là trung điểm của AE
N là trung điểm của BE
=> MN là đường trung bình ứng với cạnh AB của ΔEAB, suy ra MN // AB (1)
Gọi R là trung điểm của AD
Trong ΔADB, RQ là đường trung bình, suy ra RQ // AB
Trong ΔCAD, RP là đường trung bình, suy ra RP // DC
mà DC // AB nên RP // AB.
RQ và RP cùng đi qua R và cùng song song với AB nên theo tiên đề Ơclit thì RQ ≡ RP
Từ đây ta suy ra QP // AB (2)
Từ (1) và (2) suy ra MN // PQ => Tứ giác MNPQ là hình thang do một cặp cạnh đối song song.
– Cách 2: Chứng minh tứ giác đó có tổng hai góc kề một cạnh bên bằng 180 độ.
Ví dụ: Cho tam giác ABC. Trên AC lấy một điểm B’ sao cho AB’ = AB và trên AB lấy một điểm C’ sao cho AC’ = AC. Chứng minh tứ giác BB’CC’ là hình thang.
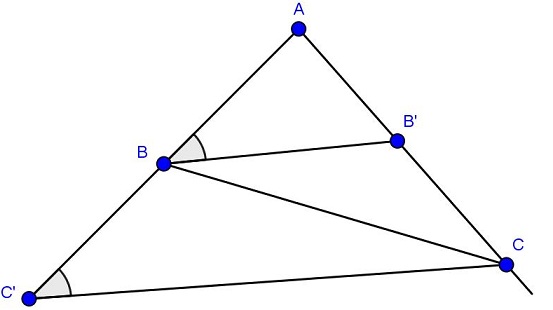
Ta có:
AB’ = AB
=> ∆BAB’ cân tại A
=> Góc ABB’ = (180°- Â)/2
Chứng minh tương tự, ta có: Góc AC’C = (180°- Â)/2
=> Góc ABB = Góc AC’C
=> Góc ABB’ + Góc B’BC’ = Góc AC’C + Góc B’BC’
=> Góc AC’C + Góc B’BC’ = 180°
=> Tứ giác BB’CC’ là hình thang do tổng hai góc kề một cạnh bên bằng 180°
III. BÀI TẬP VỀ CHỨNG MINH HÌNH THANG
Bài 1 : Cho hình thang vuông ABCD có A = D = 90o, C = 45o. Biết đường cao bằng 4cm, AB + CD = 10 cm, tính hai đáy.
Bài 2: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE.
a) Tứ giác BDEC là hình gì? Vì sao?
b) Tính các góc của hình thang BEDC, biết A = 70o.
c) Các điểm D, E ở vị trí nào thì BD = DE = EC?
Bài 3 : Hình thang ABCD (AB//CD) có A – D = 20o, B = 2C . Tính các góc của hình thang.
Giải.
Vì ABCD là hình thang (AB//CD), nên ta có :
B + C = 180o (hai góc trong cùng phía bù nhau)
2C + C = 180o ( vì B = 2C)
3C = 180o → C = 60o → B = 2.60o = 120o
A – D = 20o → A = 20 + D
A + D = 180o (hai góc trong cùng phía bù nhau)
20 + D + D = 180
2D = 160 → D = 80 →à A = 20 + 80 = 100
Vậy A = 100 ; B = 120 ; C = 60 ; D = 80.
Bài 4 : Tính các góc của hình thang ABCD (AB // CD) biết A = 3D và B – C = 30.
Gợi ý : Vẽ hình tượng trưng và làm như bài toán 1.
Bài 5: Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng từ giác ABCD là hình thang.
Gợi ý :
AB = BC để làm gì?
AC là tia phân giác để làm gì?
Bài 6: Tứ giác ABCD có BC = CD và BD là tia phân giác của góc D. Chứng minh rằng ABCD là hình thang.
Gợi ý : vẽ hình và làm tương tự bài toán 3.
Cách chứng minh một tứ giác là hình thang à chứng minh 2 cạnh song song à 2 góc đồng vị bằng nhau, so le trong bằng nhau hoặc trong cùng phía bù nhau.
Bài 7: Tính các góc của hình thang ABCD biết A = 60o và C = 130o.
Gợi ý : Dựa vào tính chất : ABCD là hình thang → 2 đáy song song → 2 góc trong cùng phía bù nhau.
Bài 8: Tính các góc của hình thang ABCD biết A = 50o và C = 120o.
BàI 9 : Hình thang vuông ABCD có A = D = 90o, C = 45o . Biết đường cao bằng 4cm. AB + CD = 10cm, Tính hai đáy.
Gợi ý :
- Vẽ hình
- Đường cao AD = 4cm.
- Dựng đường cao BH à BH = AB = 4cm.
- Tam giác BHC vuông tại H và C = 45o à tam giác BHC là tam giác vuông cân à BH = CH = 4cm.
- AB + CD = 10
AB + DH + CH = 10
AB + AB + 4 = 10 (vì AB = DH)
2AB = 6 → AB = 3 → DH = 3 → DC = DH + CH = 3 + 4 = 7cm.
Bài 10: Tính các góc của hình thang cân ABCD (AB // CD), biết D = 2A.
Gợi ý : AB // CD à A và D là hai góc trong cùng phía bù nhau à A + D = 180
Bài 11: Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D
AC, E AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Gợi ý :
Bước 1 : Chứng minh tứ giác BEDC là hình thang (hai góc đồng vị AED = ABC tính thông qua góc chung A của 2 tam giác cân ABC và tam giác cân AED à chứng minh tam giác AED là tam giác cân à chứng minh AE = AD)
Bước 2 : BEDC là hình thang dễ dàng thấy B = C (vì tam giác ABC cân tại A) à là hình thang cân.
Bài 12 : Cho hình thang cân ABCD, có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng AC là tia phân giác của góc C.
Gợi ý :
ABCD là hình thang cân, đáy nhỏ AB
AB = AD (gt)
BC = AD (vì ABCD là hình thang cân)
Nên tam giác ABC cân tại B à học sinh tự tư duy tiếp.
Bài 13 : Cho tam giác ABC cân tại A. Trên cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.
a) Chứng minh tứ giác BMNC là hình thang cân.
b)Tính các góc của tứ giác BMNC biết rằng A = 40o.
Gợi ý : tứ giác BMNC là hình thang cân BMNC là hình thang (đồng vị, so le trong, trong cùng phía bù nhau) hình thang cân (2 cách chứng minh hình thang cân).
Bài14 : Cho tam giác ABC cân tại A. Trên tia đối của AC lấy điểm D, trên tia đối của AB lấy điểm E sao cho AD = AE. Chứng minh tứ giác BDEC là hình thang cân.
Gợi ý :
Bài15 : Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho CM = CA. Đường thẳng đi qua M và song song với CA cắt AB tại I.
a) Tứ giác ACMI là hình gì ?
b) Chứng minh AB + AC < AH + BC.
Bài16 : Cho tam giác ABC, các tia phân giác của góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt cạnh AB và AC tại D và E.
a) Vẽ hình và tìm các hình thang trong hình vẽ.
b) Chứng minh rằng hình thang BCED có một cạnh đáy bằng tổng hai cạnh bên.
Gợi ý :
Bài 17 : Cho tam giác ABC có BC = 4cm, các trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm cuẩ BE, CD. Gọi giao điểm của MN với BD, CE theo thứ tự là P, Q.
a) Tính độ dài MN.
b) Chứng minh rằng MP = PQ = QN.
Trên đây, Zicxabooks.com.vn đã giới thiệu đến quý thầy cô và các bạn lí thuyết về hình thang và cách chứng minh hình thang nhanh, chính xác. Hi vọng, bài viết đã cung cấp cho bạn những thông tin hữu ích. Xem thêm các phương pháp phân tích đa thức thành nhân tử tại đường link này bạn nhé !
