Nội dung bài viết này sẽ chỉ đề cấp đến việc tổng hợp hai dao động điều hòa cùng phương cùng tần số và phương pháp giản đồ FRE NEN để tổng hợp 2 dao động cùng phương cùng tần số này. Qua đó chúng ta sẽ áp dụng giải một số bài tập để hiểu rõ hơn.
I. Vectơ quay
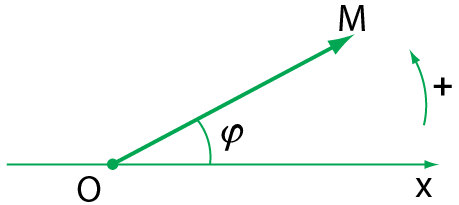
– Khi điểm M chuyển động tròn đều thì vectơ vị trí quay đều với cùng tốc độ góc ω. Khi ấy x=Acos(ωt+φ) là phương trình của hình chiếu của vectơ quay lên trục x.- Dựa vào đó đưa ra cách biểu diễn phương trình của dao động điều hòa bằng một vectơ quay được vẽ tại thời điểm ban đầu như hình minh họa ở trên.
• Vectơ quay có những đặc điểm sau đây:
– Có gốc tại gốc tọa độ của trục Ox
– Có độ dài bằng biên độ dao động, OM = A;
– Hợp với trục Ox một góc bằng pha ban đầu (chọn chiều dương là chiều dương của đường tròn lượng giác).
II. Phương pháp giản đồ FRE-NEN
1. Đặt vấn đề
– Phương pháp giản đồ Fre-nen thường được dùng để tìm li độ của dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số nhưng khác biên độ dao động (A1 ≠ A2) như sau:
x1=A1cos(ωt+φ1)
x2=A2cos(ωt+φ2)
2. Phương pháp giản đồ Fre-nen tổng hợp 2 dao động điều hòa
– Vẽ hai vectơ quay và 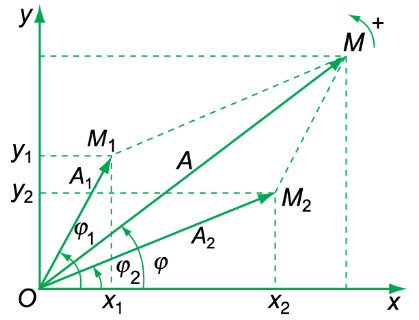 , vẽ vectơ là tổng của hai vectơ và
, vẽ vectơ là tổng của hai vectơ và  như hình sau:
như hình sau:
x1 = A1cos(ωt+φ1)
x2 = A2cos(ωt+φ2)
⇒ x = Acos(ωt+φ)
– Như vậy, dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số là một dao động điều hòa cùng phương, cùng tần số với hai dao động đó.
– Trong trường hợp tổng quát, biên độ và pha ban đầu của dao động tổng hợp được tính bằng các công thức sau đây:
3. Ảnh hưởng của độ lệch pha
– Từ công thức trên ta thấy biên độ của dao động tổng hợp phụ thuộc vào các biên độ A1, A2 và độ lệch pha (φ2-φ1) của các dao động thành phần.
– Nếu các dao động thành phần cùng pha, tức ∆φ = φ2 – φ1 = 2nπ, (n = 0, ±1, ±2,…), thì biên độ dao động tổng hợp là lớn nhất và bằng tổng hai biên độ: A = A1 + A2.
– Nếu hai dao động thành phần ngược pha, tức ∆φ = φ2 – φ1 = (2n+1)π, (n = 0, ±1, ±2,…), thì biên độ dao động tổng hợp là nhỏ nhất: A = |A1 – A2|
4. Ví dụ minh họa phương pháp giản đồ FRE-NEN tổng hợp 2 giao động
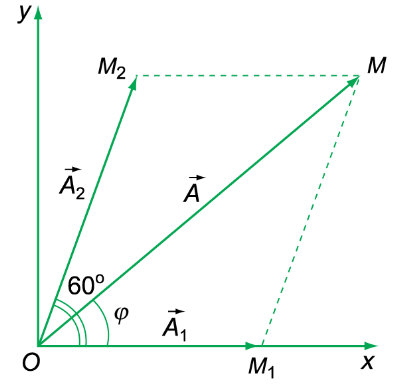
– Cho hai dao động điều hòa cùng phương, cùng tần số:
– Tìm phương trình dao động tổng hợp của 2 giao động trên.
* Lời giải: Ta vẽ hai vectơ quay biểu diễn hai dao động thành phần tại thời điểm ban đầu. – Áp dụng các công thức tính biên độ và pha của dao động tổng hợp ta có:

Vậy
⇒ Vậy phương trình của dao động tổng hợp là:
III. Bài tập về tổng hợp dao động cùng phương cùng tần số và lời giải
* Bài 1 trang 25 SGK Vật lý 12: Nêu cách biểu diễn một dao động điều hòa bằng một vecto quay.
>> Lời giải bài 1 trang 25 SGK Vật lý 12
* Bài 2 trang 25 SGK Vật lý 12: Trình bày phương pháp giản đồ Fre-nen để tìm dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số.
>> Lời giải bài 2 trang 25 SGK Vật lý 12
* Bài 3 trang 25 SGK Vật lý 12: Nêu ảnh hưởng của độ lệch pha (φ2 – φ1) đến biên độ của dao động tổng hợp trong các trường hợp:
a) Hai dao động thành phần cùng pha
b) Hai dao động thành phần ngược pha
c) Hai dao động thành phần có pha vuông góc
>> Lời giải bài 3 trang 25 SGK Vật lý 12
* Bài 4 trang 25 SGK Vật lý 12: Chọn đáp án đúng. Hai dao động là ngược pha khi:
A. φ2 – φ1 = 2nπ ;
B. φ2 – φ1 = nπ
C. φ2 – φ1 = (2n – 1)π ;
D. φ2 – φ1 = (2n + 1)π
>> Lời giải bài 4 trang 25 SGK Vật lý 12
* Bài 5 trang 25 SGK Vật lý 12: Xét một vecto quay có những đặc điểm sau:
– Có độ lớn bằng hai đơn vị chiều dài.
– Quay quanh O với tốc độ góc 1 rad/s
– Tại thời điểm t = 0, vecto hợp với trục Ox một góc 30o
Hỏi vecto quay biểu diễn phương trình của dao động điều hòa nào?
A. x = 2cos(t – π/3)
B. x = 2cos(t + π/6)
C. x = 2cos(t – 30o)
D. x = 2cos(t + π/3)
>> Lời giải bài 5 trang 25 SGK Vật lý 12